Machine Learning
Linear regression:
Logistic regression:
Logistic regression:
SVM:
Convex Optimization: achieves global minimum, no local traps
Convex Sets: x1, x2 in C, 0<= t <=1 ==> t*x1 + (1-t)*x2 in C
Gradient Descent: Use for unconstrained optimization min(x) f(x)
Main idea: take a step proportional to the negative of the gradient
Extremely popular; simple and easy to implement
Handful of approaches to selecting step size:
1) fixed step size
2) exact search
3) backtracking line search
Limitations of Gradient Descent:
Step size search may be expensive;
Convergence is slow for ill-conditioned problems;
Convergence speed depends on initial starting position;
Does not work for non differentiable or constrained problems.
Linear Regression Formulation:
Given an inout vector X' = (X1, X2, ..., Xp), we want to predict the quantitative response y.
Minimize sum of square errors: (Objective function)
Least square solutions:)
Outcome vector is orthogonally projected onto hyperplane spanned by input features
Measure of Fit: R^2
Easy interpretation: the percentage of variation in data explained by the model:
Closer to 1 means the better the fit.
How certain are we about our model and the parameters?
Probability Interpretation:
Assume data is generated from probability model
Maximum Likelihood Estimator
Model Assumptions:
Conditional mean of y is linear in the predictor variables
Error terms are normally distributed (Gaussian)
Variance Estimate:
Conditional distribution of Y is normal:
Variance estimate(regression standard error):
Standard deviation or standard error determines how close estimator is to true value.
Regression: Basis Functions
Generalize features to basis functions
Special case: linear regression, polynomial regression
Feature selection:
Selecting the best features
Stepwise selection:
Forward: start with 0 and sequentially add feature that best improves fit, can be used whenever
Backward: start with full model, remove feature that is least detrimental to fit, can only be used when N>p
Regularization:
Add penalty term on model parameters to achieve a more simple model or reduce sensitivity to training data:
Reasons: less prone to overfitting, get the right model complexity
Popular Penalties:
Ridge Regularization:
discourage large values
also known as shrinkage or weight decay
closed form solution
Lasso Regularization:
Subtle difference from the ridge is the use of the 1-norm
Large values drive coefficients to zero
No closed form solution but efficient algorithms exist with approximately same computational cost as ridge
Lasso = Least Absolute Selection and Shrinkage Operator
NOTEs:
If intercept term is included in regression, this coefficient is left unpenalized, usually center the columns of X to exclude intercept;
Penalty term can be unfair if predictors are on different scales, scale columns of X to have same sample variance
What happens if none of the coefficients are small?
Regularization may still help as it greatly reduces the variance of our prediction while introducing some bias.
Elastic Net Regularization:
Selects variables like lasso
Shrinks coefficients of correlated predictions like ridge
Computational advantages over general Lq penalties.
Bayesian Linear Regression:
What if we want to know the distribution over the coefficients and the variance?
What if we want to quantify uncertainty?
What if we have lots of outliers?
What if we have a prior?
Assume observations with Gaussian noise:
Given observe data, likelihood function:
Define a conjugate prior over coefficients:
Combine with likelihood function:
















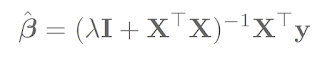






Comments
Post a Comment